二分查找
二分查找也称为折半查找,每次都能将查找区间减半,这种折半特性的算法时间复杂度都为 O(logN)。
左闭右闭
//nums是数组,size是数组的大小,target是需要查找的值
//写法一:左闭右闭
int search(int nums[], int size, int target) {
int left = 0;
int right = size - 1; // 定义了target在左闭右闭的区间内,[left, right]
while (left <= right) { //当left == right时,区间[left, right]仍然有效
int middle = left + ((right - left) / 2);//等同于 (left + right) / 2,防止溢出
if (nums[middle] > target) {
right = middle - 1; //target在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; //target在右区间,所以[middle + 1, right]
} else { //既不在左边,也不在右边,那就是找到答案了
return middle;
}
}
//没有找到目标值
return -1;
}
① 查找33,那么target 的值就是33
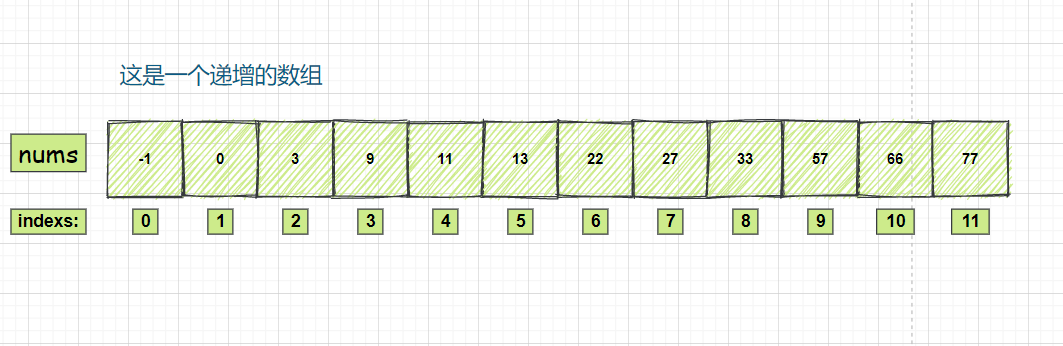
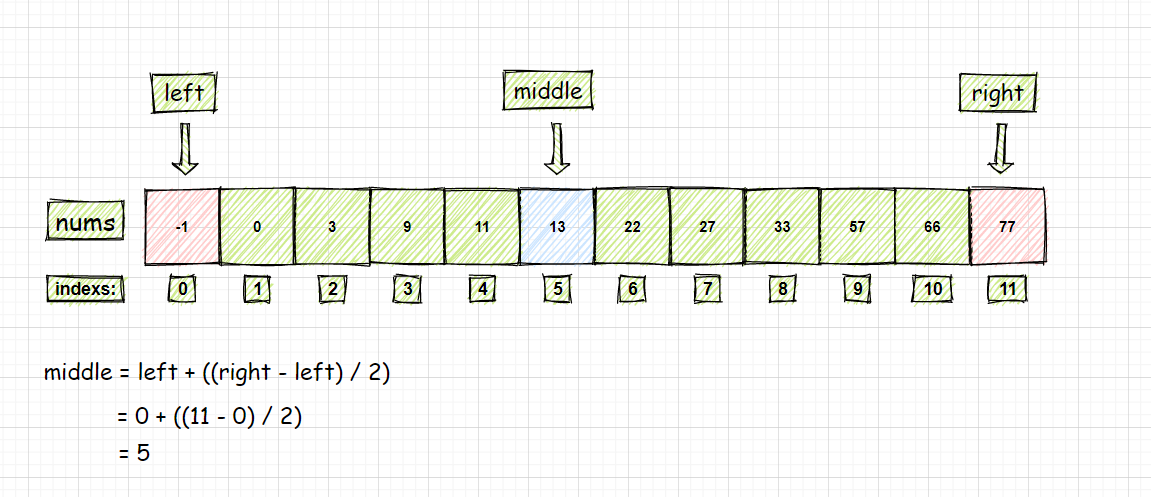
② left = 0 ; right = 11 ; middle = left + ( (right - left ) / 2 ) = 5;
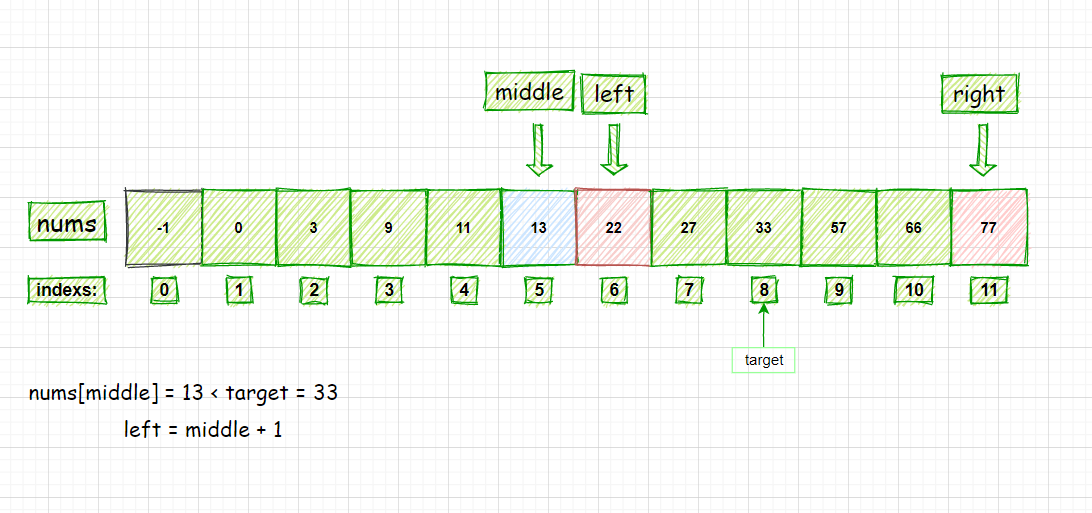
③ nums[5] < 33 ; left = middle +1 = 6 ;
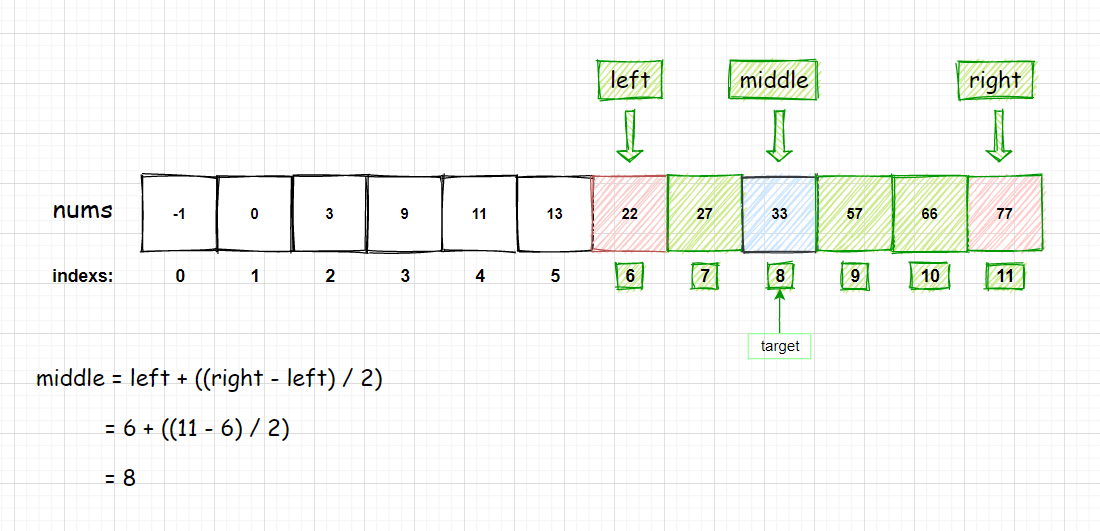
④ middle = left + ( (right - left ) / 2 ) = 8 ; nums[middle]== target
左闭右开
//写法二:左闭右开
int search(int nums[], int size, int target){
int left = 0;
int right = size; //定义target在左闭右开的区间里,即[left, right)
while (left < right) { //因为left = right的时候,在[left, right)区间上无意义
int middle = left + ((right - left) / 2);
if (nums[middle] > target) {
right = middle; //target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1;
} else {
return middle;
}
}
// 没找到就返回-1
return -1;
}
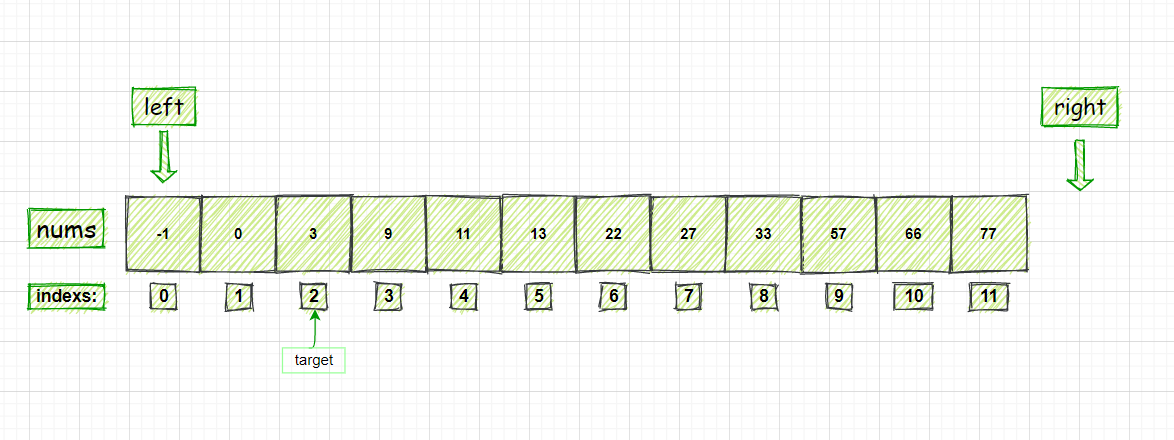
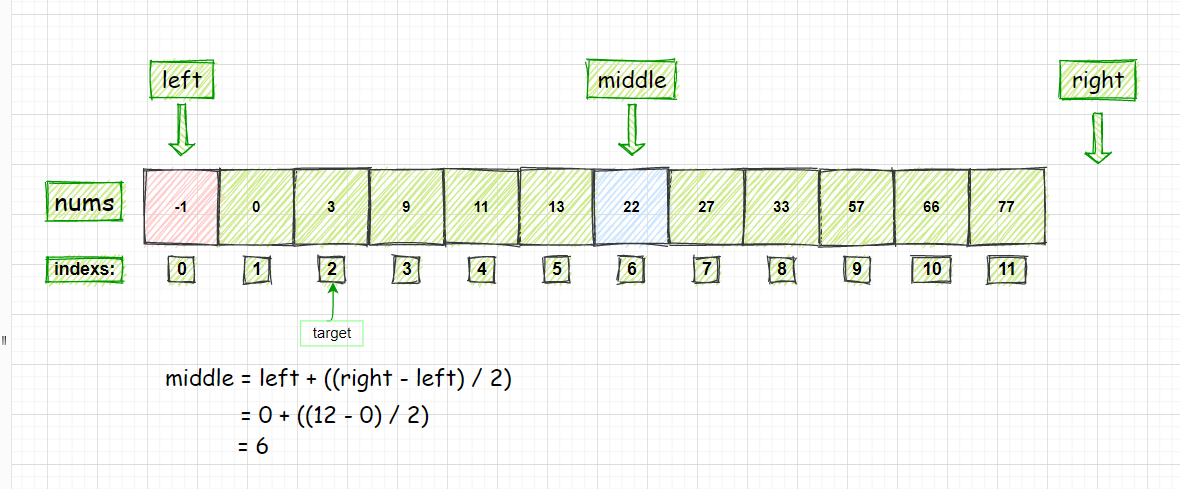
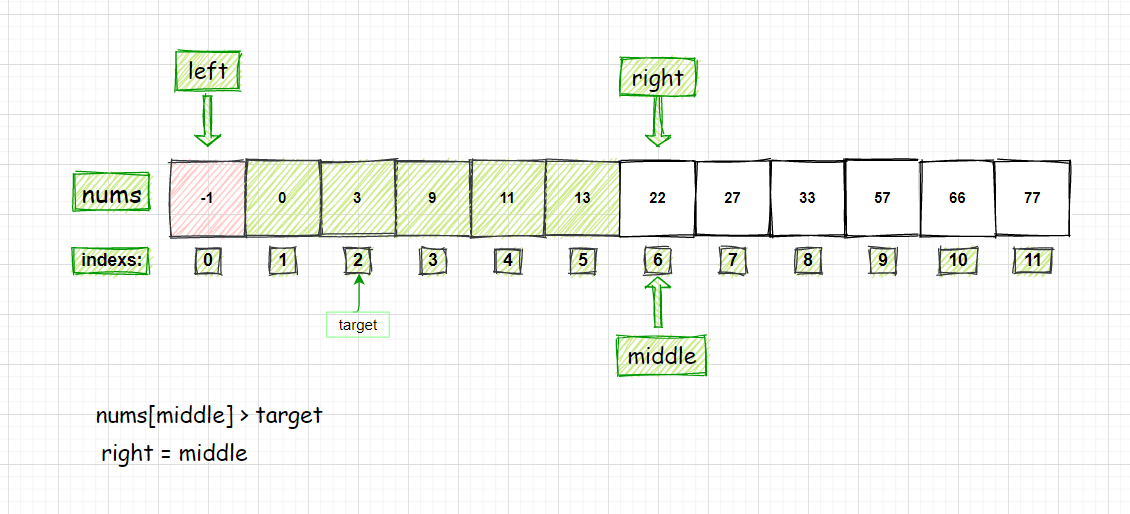
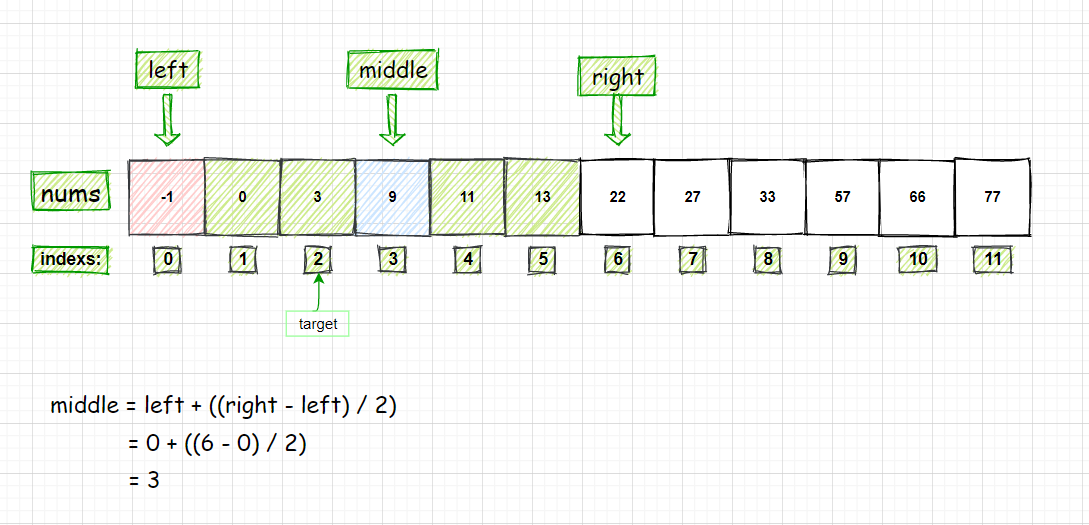
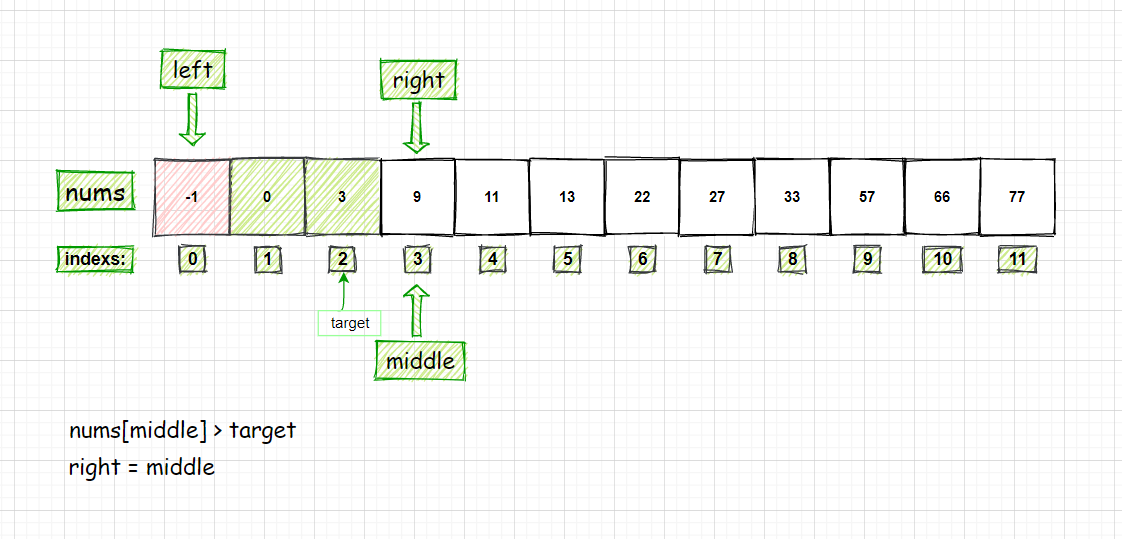
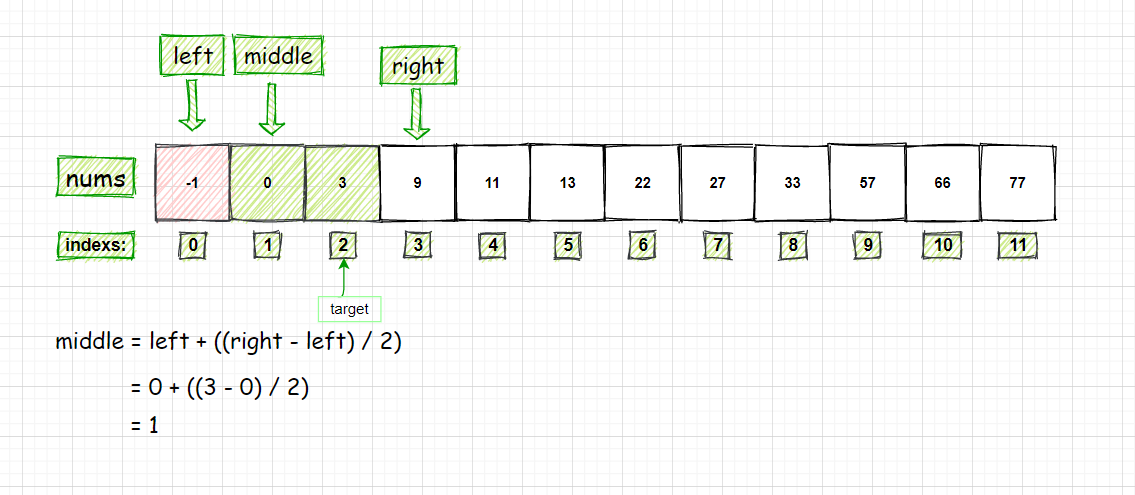
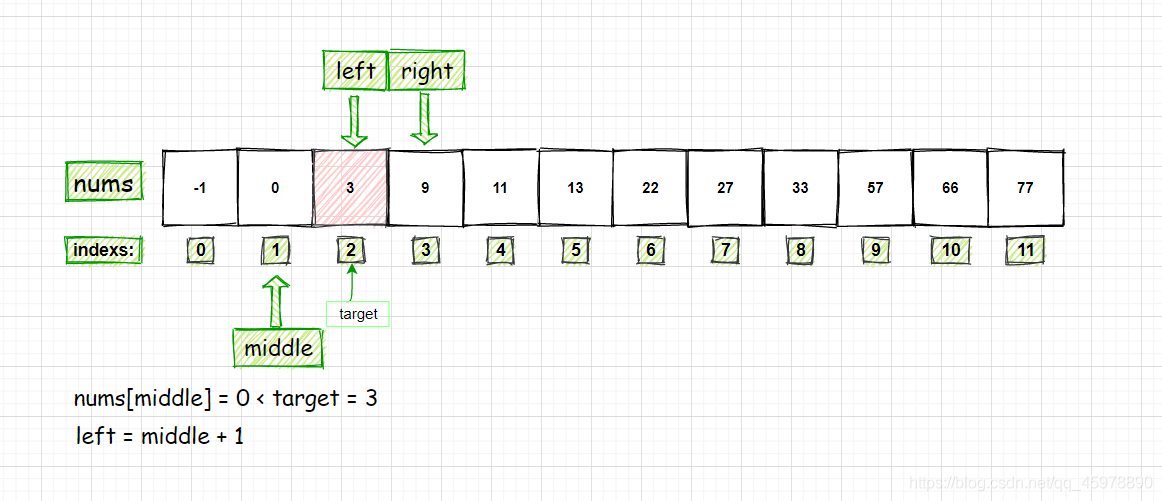
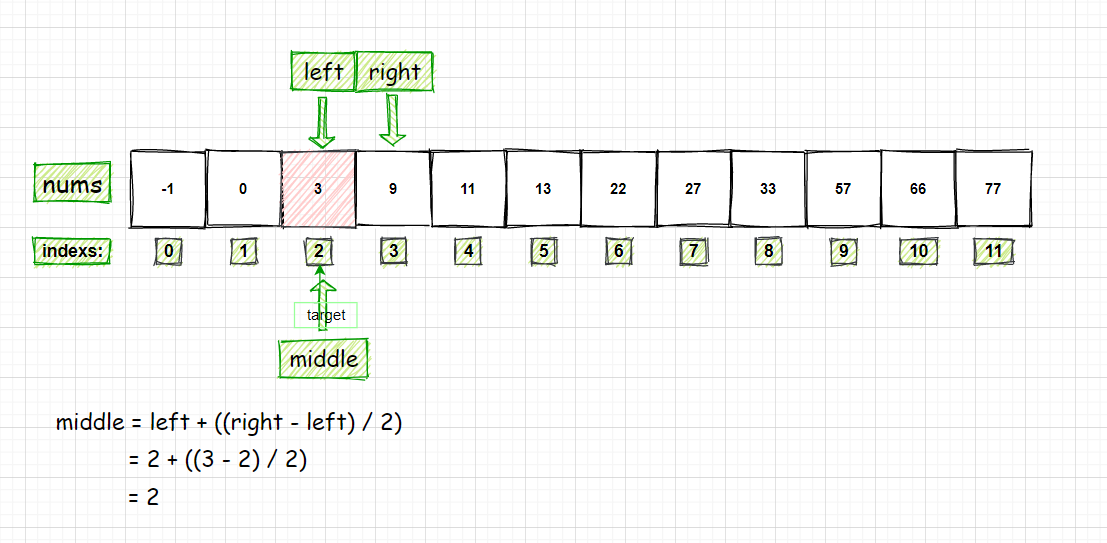
查找的数字为29的算法过程分析:
① int nums[] = {1,5,9,11,23,29,31};l = 0,h = 6
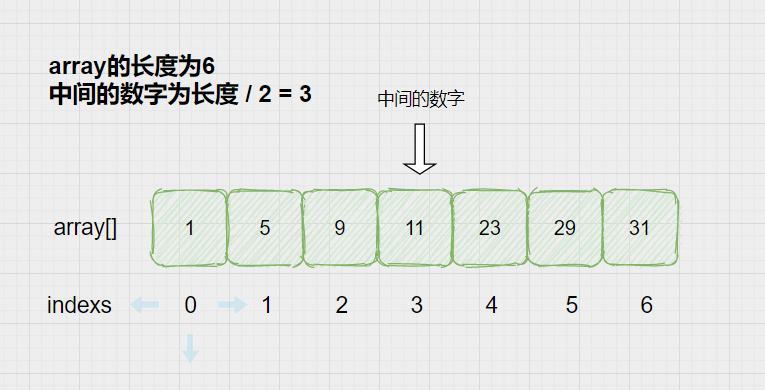
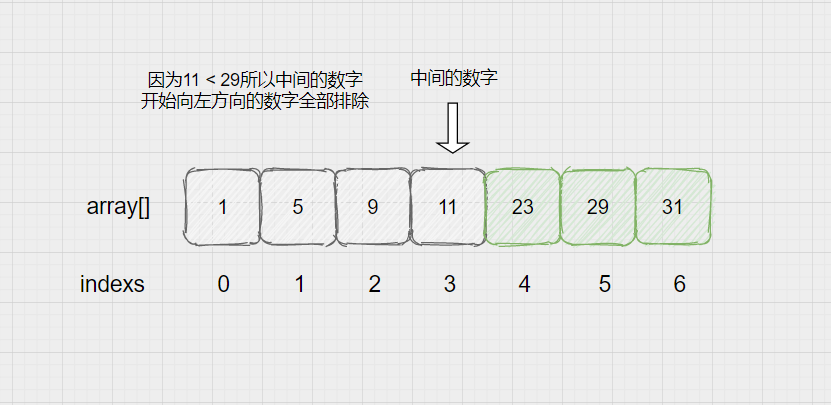
② 29 > 11,所以左边的所有数字全部排除
参考文章:


评论区