排序算法

1、排序的基本概念

排序：重新排列表中的元素，使表中元素满足按关键字有序的过程（关键字可以相同）
排序算法的评价指标：时间复杂度、空间复杂度；
排序算法的稳定性：关键字相同的元素在排序之后相对位置不变，称为稳定的；
Q：稳定的排序算法一定比不稳定的好？
A：不一定，要看实际需求；
排序算法的分类：
- 内部排序：数据都在内存——关注如何使时间、空间复杂度更低；
- 外部排序：数据太多，无法全部放入内存——关注如何使时间、空间复杂度更低，如何使读/写磁盘次数更少；

2、插入排序

2.1 直接插入

算法过程描述：

把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

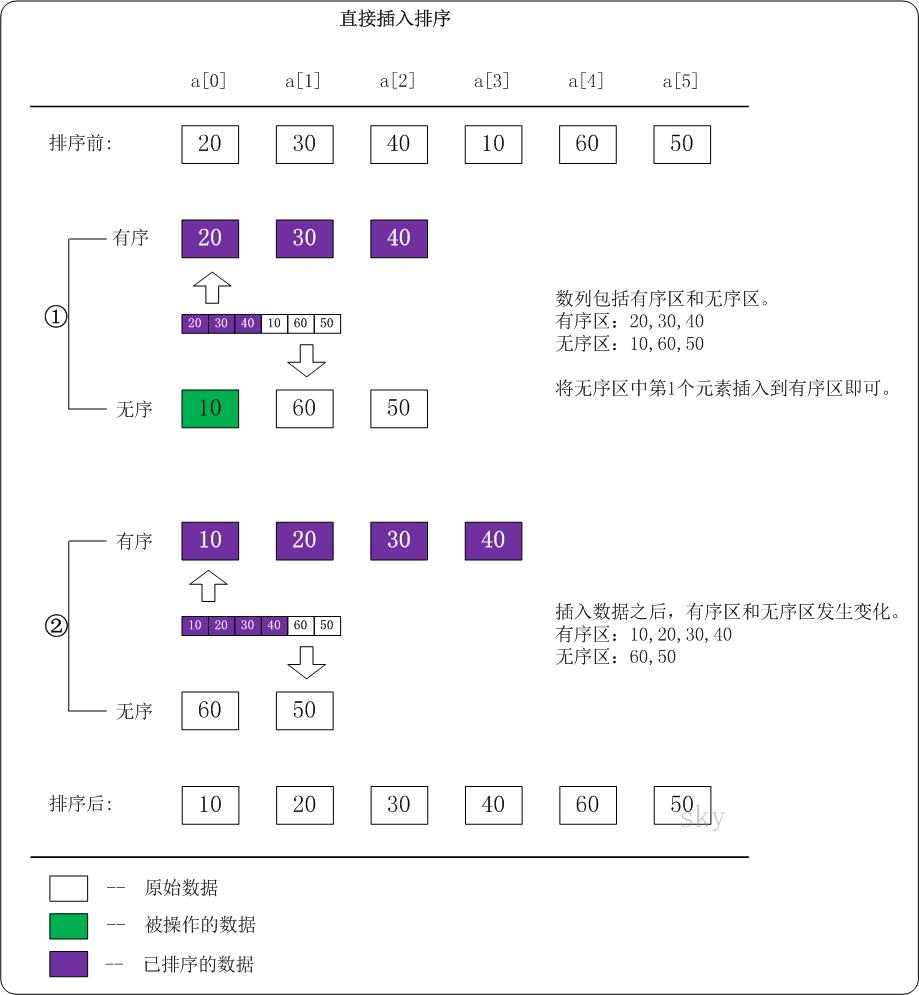
代码实现：

/**
 * 插入排序
 * @param arr 待排序列
 * @param n 待排序列元素个数
 */
void InsertSort(int arr[], int n) {
    int i, j, tmp;
    for (i = 1; i < n ; i++) {
        // 关键字小于前驱
        if (arr[i] < arr[i - 1]) {
            // 从无序列表中取出第一个元素
            tmp = arr[i];
            for ( j = i - 1; j >= 0 && arr[j] > tmp; --j) {
                // 所有大于temp的元素都向后挪
                arr[j + 1] = arr[j];
            }
            // 一趟排序完成说明已将无序表中的第一个元素移到了有序表中合适位置了
            arr[j + 1] = tmp;
        }
    }
}

算法效率分析：

空间复杂度：O(1)
时间复杂度：主要来自于对比关键字、移动关键字，若有n个元素，则需要n-1躺处理
- 最好情况： 原本为有序，共n-1趟处理，每一趟都只需要对比1次关键字，不需要移动元素，共对比n-1次 —— O(n)
- 最差情况： 原本为逆序 —— O(n²)
- 平均情况： O(n²)
算法稳定性：稳定

2.2 折半插入

算法过程描述

先用折半查找找到应该插入的位置，再移动元素；
为了保证稳定性，当查找到和插入元素关键字一样的元素时，应该继续在这个元素的右半部分继续查找以确认位置; 即当 A[mid] == A[0] 时，应继续在mid所指位置右边寻找插入位置
当 low > high 时，折半查找停止，应将 [low,i-1]or[high+1,i-1]内的元素全部右移，并将A[0]复制到low所指的位置；

代码实现

算法效率分析

与直接插入排序相比，比较关键字的次数减少了，但是移动元素的次数没有变，时间复杂度仍然是O(n²)

2.3 希尔排序

算法过程描述

代码实现

算法效率分析

空间复杂度：
时间复杂度：

3、交换排序

基本思想：基于交换的排序，根据序列中两个元素关键字比较结果来交换位置

3.1 冒泡排序

算法过程描述

每一趟冒泡的结果都是把序列中最小元素放到序列的最终位置。这样只需n - 1 趟冒泡就能把所有元素排好序。
为保证稳定性，关键字相同的元素不交换；

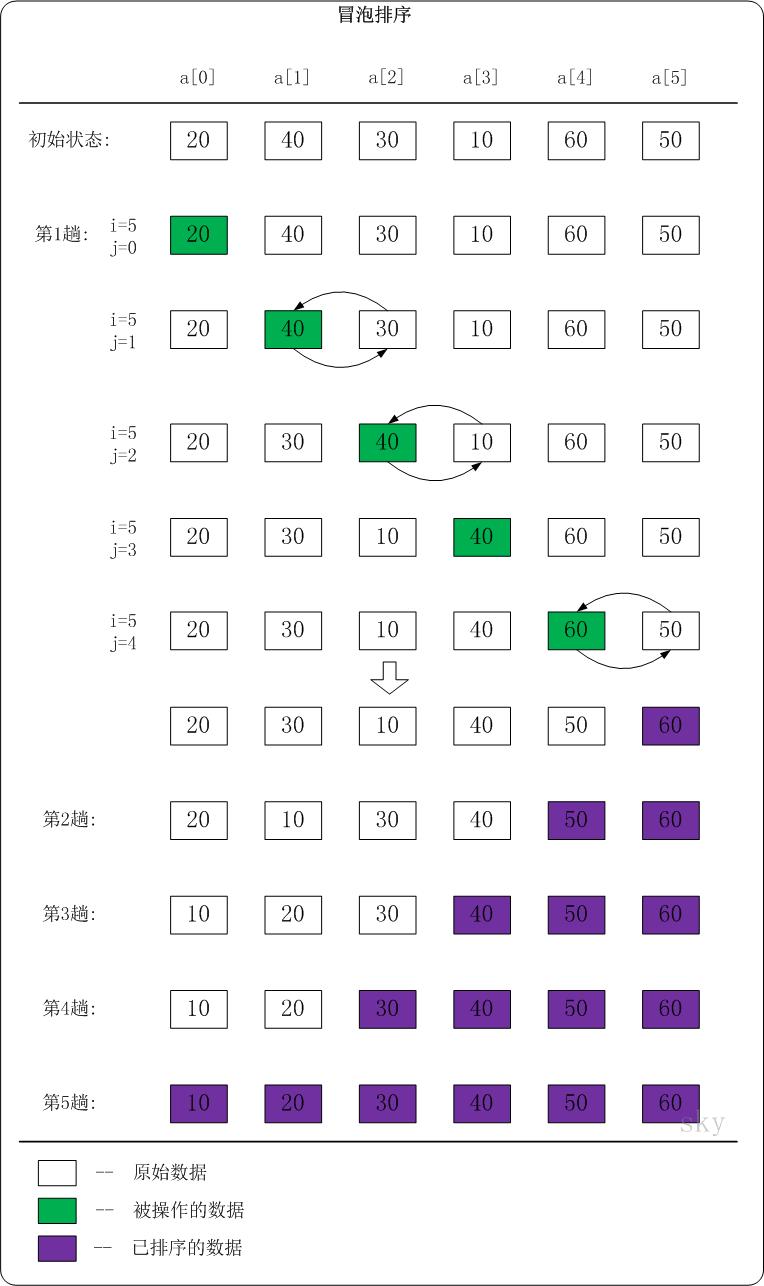
代码实现

/**
 * 交换两个元素
 * @param a
 * @param b
 */
void swap(int &a, int &b) {
    int tmp = a;
    a = b;
    b = tmp;
}

/**
 * 冒泡排序
 * @param arr : 待排序列
 * @param n ：序列个数
 */
void BubbleSort(int arr[], int n) {
    // n - 1 趟排序
    for (int i = 0; i < n - 1; ++i) {
        // 标识本趟冒泡是否交换
        bool flag = false;
        // 每一趟冒泡比较的过程
        for (int j = n - 1; j > i; j--) {
            if (arr[j - 1] > arr[j]) {
                swap(arr[j - 1], arr[j]);
                flag = true;
            }
        }
        // 如果本趟遍历后没有发生交换，说明表已经有序，可以结束算法
        if (flag) {
            return;
        }
    }
}

算法效率分析

空间复杂度：O(1)
时间复杂度：
- 最好情况 (有序) ：只需要一趟排序，比较次数=n-1，交换次数=0，最好时间复杂度=O(n)
- 最坏情况 (逆序) ：比较次数 = (n-1)+(n-2)+…+1 = n(n-1)/2 = 交换次数，最坏时间复杂度 = O(n²)
- 平均时间复杂度 = O(n²)
稳定性：稳定

3.2 快速排序

算法过程描述

选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分；其中一部分的所有数据都比另外一部分的所有数据都要小。然后，再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

每一趟排序都可使一个中间元素确定其最终位置
用一个元素（不一定是第一个）把待排序序列“划分”为两个部分，左边更小，右边更大，该元素的最终位置已确认

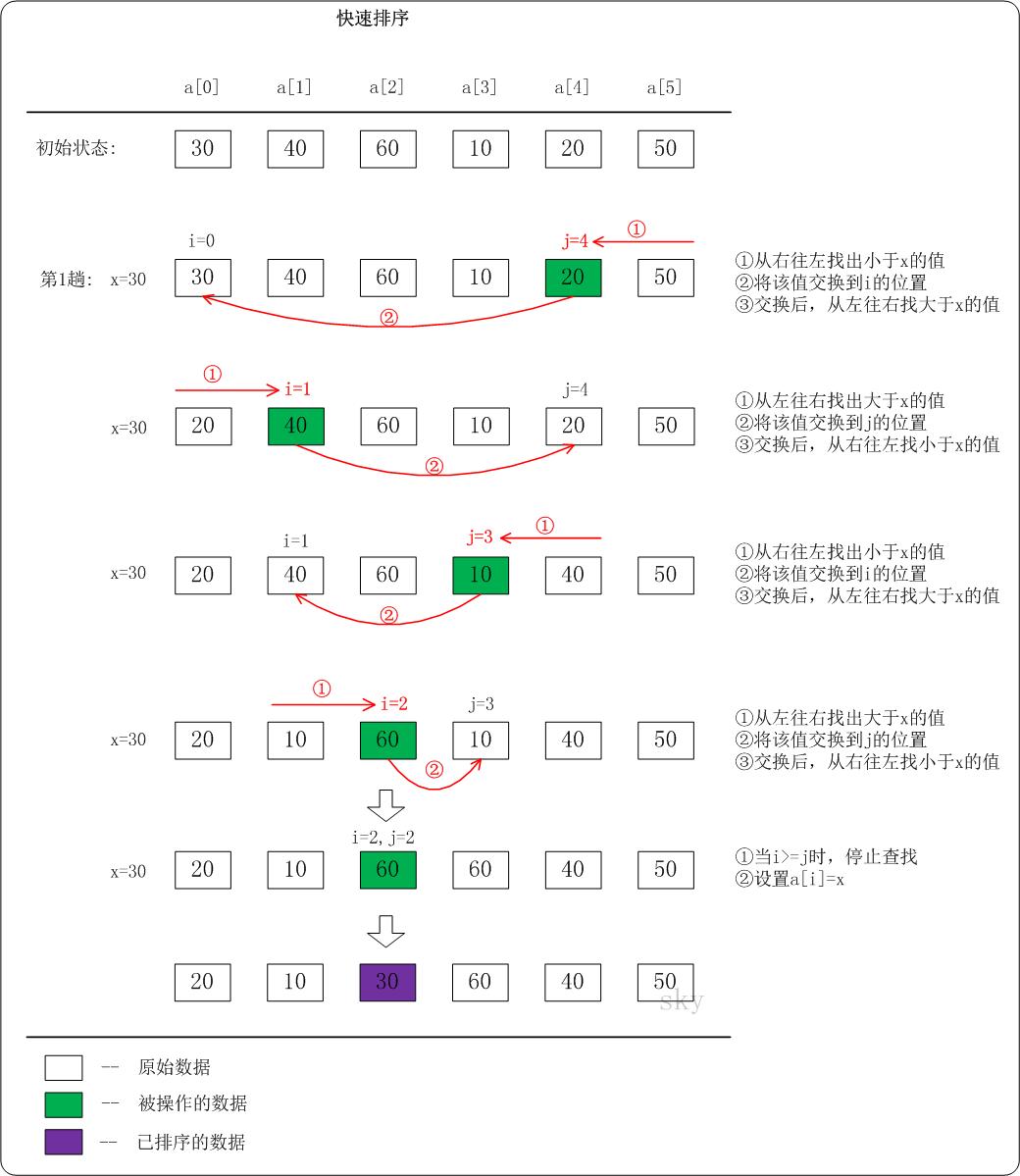
代码实现

算法效率分析

每一层的QuickSort只需要处理剩余的待排序元素，时间复杂度不超过O(n);
把n个元素组织成二叉树，二叉树的层数就是递归调用的层数，n个结点的二叉树最小高度 = ⌊log₂n⌋ + 1, 最大高度 = n
空间复杂度 ：O(递归层数)（递归层数最小为log₂n）
- 最好 = O(log₂n)
- 最坏 = O(n)
时间复杂度：O(n×递归层数) （递归层数最大为n）
- 最好 = O(nlog₂n) : 若每一次选中的“枢轴”可以将待排序序列划分为均匀的两个部分，则递归深度最小，算法效率最高；
- 最坏 = O(n²) ：序列本就有序或逆序，此时时间、空间复杂度最高；
稳定性：不稳定
快速排序使所有内部排序算法中平均性能最优的排序算法；
快速排序算法优化思路： 尽量选择可以把数据中分的枢轴元素
- 选头、中、尾三个位置的元素，取中间值作为枢轴元素；
- 随机选一个元素作为枢轴元素；

4、选择排序

4.1 简单选择排序

算法过程描述

每一趟在待排元素中找到最小元素加入有序子序列的末尾，n 个元素只需 n - 1趟处理

代码实现

算法效率分析

空间复杂度：
时间复杂度：

4.2 堆排序

算法过程描述

代码实现

算法效率分析

空间复杂度：
时间复杂度：

5、归并排序

算法过程描述

代码实现

算法效率分析

空间复杂度：
时间复杂度：

6、基数排序

算法过程描述

代码实现

算法效率分析

7、总结

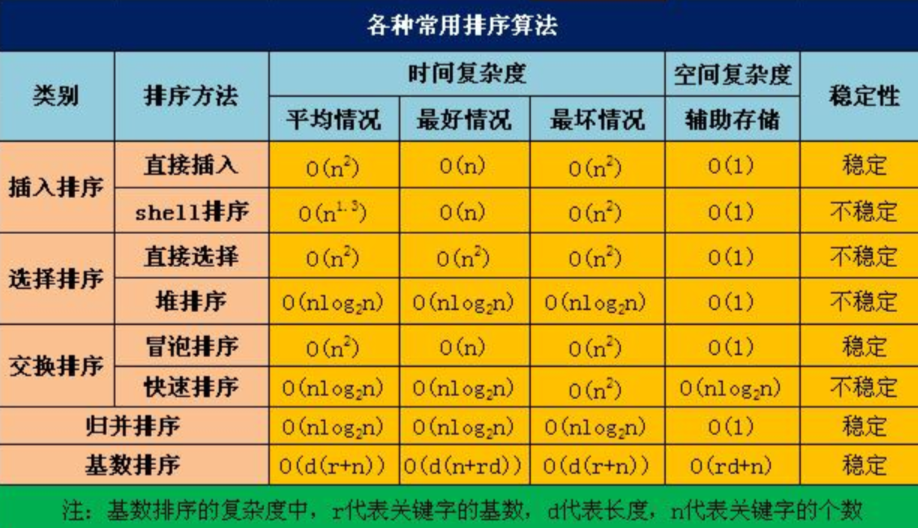
稳定的排序算法：
不稳定的排序算法：

参考：

https://www.pdai.tech/md/algorithm

https://blog.csdn.net/weixin_45016439/article/details/115742183

目录CONTENT

排序算法

1、排序的基本概念

2、插入排序

2.1 直接插入

2.2 折半插入

2.3 希尔排序

3、交换排序

3.1 冒泡排序

3.2 快速排序

4、选择排序

4.1 简单选择排序

4.2 堆排序

5、归并排序

6、基数排序

7、总结

评论区