数组和广义表

1、数组的顺序存储结构

数组是一种特殊的线性存储结构，它不会对内部的元素做插入和删除操作，有可能做查找（读取）和修改操作。因此，我们经常选用顺序存储结构（顺序表）来实现数组，而不用链式结构（链表）。

数组可以是多维的，而顺序表只能是一维的线性空间。要想将 N 维的数组存储到顺序表中，可以采用以下两种方案：

1. 以列序为主（先列后行）：按照行号从小到大的顺序，依次存储每一列的元素；
2. 以行序为主（先行后序）：按照列号从小到大的顺序，依次存储每一行的元素。

LOC(i, j) 为 ai,j 在内存中的地址，LOC(0, 0) 为二维数组在内存中存放的起始位置（也就是 a0,0 的位置）。

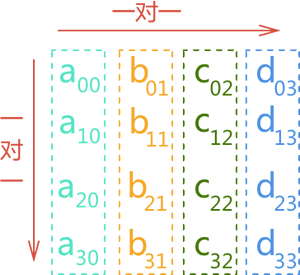
以列序为主的方案存储时，数组中的元素在顺序表中的存储状态如下图所示：

$$a_n,_m中查找 a_i,_j 公式：LOC(i, j) = LOC(0, 0) + (j * n + i) * L;$$

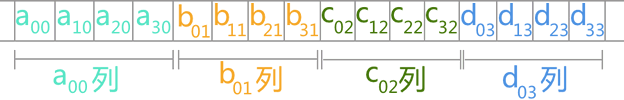
以行序为主的方案存储数组时，各个元素在顺序表中的存储状态如下所示：

$$a_n,_m中查找 a_i,_j 公式：LOC(i, j) = LOC(0, 0) + (i * m + j) * L;$$

2、特殊矩阵

特殊矩阵：

• 含有大量相同数据元素的矩阵，比如对称矩阵；
• 含有大量 0 元素的矩阵，比如稀疏矩阵、上（下）三角矩阵

压缩存储思想是：矩阵中的相同数据元素（包括元素 0）只存储一个。

2.1 对称矩阵

数据元素沿主对角线对应相等，这类矩阵称为对称矩阵。

矩阵中有两条对角线，其中从左上角到右下角的对角线称为主对角线，另一条的对角线为副对角线。对称矩阵指的是各数据元素沿主对角线对称的矩阵。

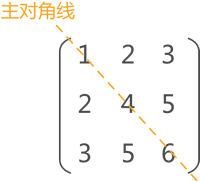
对称矩阵的实现过程是，若存储下三角中的元素，只需将各元素所在的行标 i 和列标 j 代入下面的公式：

$$k=\frac{i*(i-1)}{2} +j-1$$

存储上三角的元素要将各元素的行标 i 和列标 j 代入另一个公式：

$$k=\frac{j*(j-1)}{2} +i-1$$

2.2 上 / 下三角矩阵

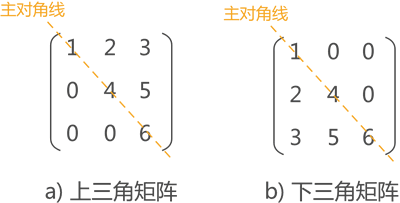
如图 4 所示，主对角线下的数据元素全部相同的矩阵为上三角矩阵（图 4a)），主对角线上元素全部相同的矩阵为下三角矩阵（图 4b)）。

对于这类特殊的矩阵，压缩存储的方式是：上（下）三角矩阵采用对称矩阵的方式存储上（下）三角的数据（元素 0 不用存储）。

例如，压缩存储图 4a) 中的上三角矩阵，矩阵最终的存储状态同图 3 相同。因此可以得出这样一个结论，上(下)三角矩阵存储元素和提取元素的过程和对称矩阵相同。

2.3 稀疏矩阵

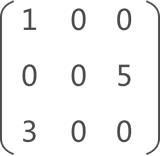
如图 5 所示，如果矩阵中分布有大量的元素 0，即非 0 元素非常少，这类矩阵称为稀疏矩阵。

压缩存储稀疏矩阵的方法是：只存储矩阵中的非 0 元素，与前面的存储方法不同，稀疏矩阵非 0 元素的存储需同时存储该元素所在矩阵中的行标和列标。

例如，存储图 5 中的稀疏矩阵，需存储以下信息：

• (1,1,1)：数据元素为 1，在矩阵中的位置为 (1,1)；
• (3,3,1)：数据元素为 3，在矩阵中的位置为 (3,1)；
• (5,2,3)：数据元素为 5，在矩阵中的位置为 (2,3)；
• 除此之外，还要存储矩阵的行数 3 和列数 3；

3、稀疏矩阵压缩存储

3.1 三元组顺序表

3.2 行逻辑链接的顺序表

3.3 十字链表

4、广义表

数组可以存储不可再分的数据元素（如数字 5、字符 ‘a’），也可以继续存储数组（即 n 维数组），但需要注意的是，以上两种数据存储形式绝不会出现在同一个数组中。而广义表中既可以存储不可再分的元素，也可以存储广义表。

4.1 广义表的定义

广义表，又称列表，也是一种线性存储结构。形如：LS = (a1,a2,…,an)，其中，LS 代表广义表的名称，an 表示广义表存储的数据。广义表中每个 ai 既可以代表单个元素，也可以代表另一个广义表。

4.2 原子和子表

广义表中存储的单个元素称为 “原子”，而存储的广义表称为 “子表”。例如，广义表 LS = {1,{1,2,3}}，则此广义表的构成 ：广义表 LS 存储了一个原子 1 和子表 {1,2,3}。

以下是广义表存储数据的一些常用形式：

• A = ()：A 表示一个广义表，只不过表是空的。
• B = (e)：广义表 B 中只有一个原子 e。
• C = (a,(b,c,d)) ：广义表 C 中有两个元素，原子 a 和子表 (b,c,d)。
• D = (A,B,C)：广义表 D 中存有 3 个子表，分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。
• E = (a,E)：广义表 E 中有两个元素，原子 a 和它本身。这是一个递归广义表，等同于：E = (a,(a,(a,…)))。

4.3 广义表的长度和深度

广义表的长度，指的是广义表中所包含的数据元素的个数。

广义表的深度就是广义表中最大的嵌套次数，是广义表中所含括号的重数。是所有子表的最大深度加1。

• A=()，长度为0，深度为1
• B=(a)，长度为1，深度为1
• C=(a,b,C)，长度为3，深度为1
• D=(a,(A),(a,(b,(c,C))),d)，长度为4，深度为4
• E=(a,(b,c),(d,(e),(f,(g))))，长度为3，深度为4

4.4 广义表的表头和表尾

当广义表不是空表时，称第一个数据（原子或子表）为"表头"，剩下的数据构成的新广义表为"表尾"。除非广义表为空表，否则广义表一定具有表头和表尾。并且广义表的表尾一定是一个广义表。

例如在广义表中 LS={1,{1,2,3},5} 中，表头为原子 1，表尾为子表 {1,2,3} 和原子 5 构成的广义表，即{{1,2,3},5}。

又如在广义表 LS = {1} 中，表头为原子 1 ，但由于广义表中无表尾元素，因此该表的表尾是一个空表，用 {} 表示。

4.5 广义表的存储结构

---

参考：

http://data.biancheng.net/