数据结构之图

1、图的定义

1.1 图的定义

图G是由集合 V 和Ｅ构成的二元组，记作G=(V,E)，其中,V是图中顶点的非空有限集合，E是图中边的有限集合。从数据结构的逻辑关系角度来看，图中任一顶点都有可能与其他顶点有关系，而图中所有顶点都有可能与某一顶点有关系。在图中，数据元素用顶点表示，数据元素之间的关系用边表示。

1.2 有向图和无向图

（1）有向图。若图中每条边都是有方向的，那么顶点之间的关系用 <Vi，Vj> 表示，它说明从 Vi 到 Vj 有一条有向边（也称为弧）。Vi 是有向边的起点，称为弧尾；Vj 是有向边的终点，称为弧头。所有边都有方向的图称为有向图。
（2）无向图。若图中的每条边都是无方向的，顶点、和之间的边用( Vi，Vj )表示。因此，在有向图中 <Vi，Vj> 与 <Vj，Vi> 分别表示两条边，而在无向图中( Vi，Vj )与( Vj，Vi )表示的是同一条边。

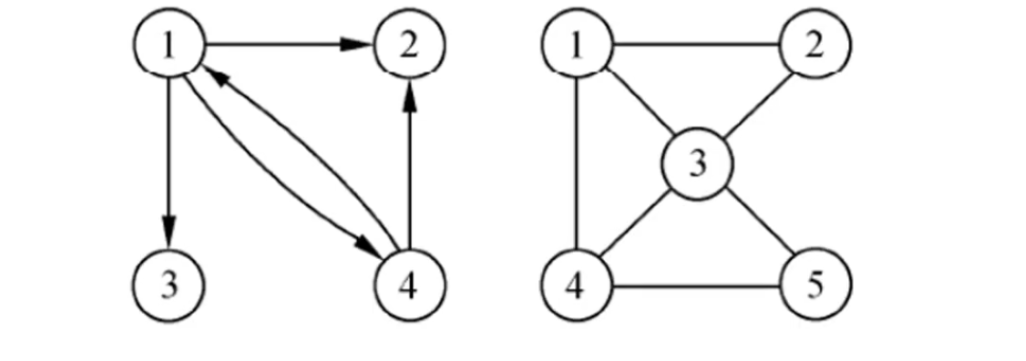
1.3 入度和出度

无向图的某个顶点的入度和出度是一样的

1.4 连通图和强连通图

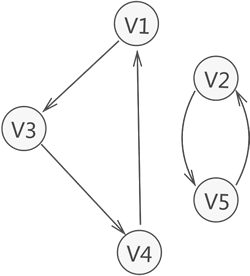
连通：从一个顶点到达另一顶点，若存在至少一条路径，则称这两个顶点是连通着的。例如图 1 中，虽然 V1 和 V3 没有直接关联，但从 V1 到 V3 存在两条路径，分别是 V1-V2-V3 和 V1-V4-V3，因此称 V1 和 V3 之间是连通的。

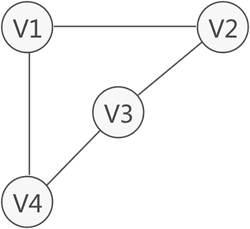
连通图：在无向图中，如果任意两个顶点之间都能够连通，则称此无向图为连通图。如下面的无向图就是一个连通图，因为此图中任意两顶点之间都是连通的。（任意两个顶点都是直接或间接连通）

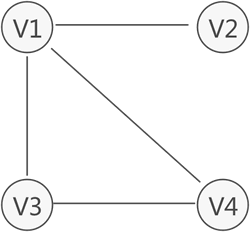
连通分量：若无向图不是连通图，但图中存储某个子图符合连通图的性质，则称该子图为连通分量。

强连通图：有向图中，若任意两个顶点 Vi 和 Vj，满足从 Vi 到 Vj 以及从 Vj 到 Vi 都连通，也就是都含有至少一条通路，则称此有向图为强连通图。下图所示就是一个强连通图。

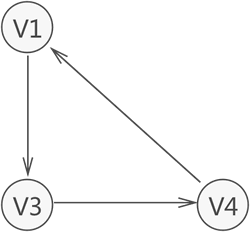
强连通分量：若有向图本身不是强连通图，但其包含的最大连通子图具有强连通图的性质，则称该子图为强连通分量。下图中，整个有向图虽不是强连通图，但其含有两个强连通分量。

• 连通图是对于无向图来说的，所以一般称为无向连通图，无向连通图的最少边是n-1，最多边是n（n-1）/2
• 强连通图是对于有向图来说的，所以一般称为有向强连通图，有向强连通图的最少边是n，最多边是n（n-1）

1.5 完全图

具有 n 个顶点的完全图，图中边的数量为 n(n-1) / 2；

具有 n 个顶点的有向完全图，图中弧的数量为 n(n-1)。

1.6 网

网就是每条边上都带有权的图叫做网。那些这些权值就需要保存下来。

2、图的存储结构

2.1 邻接矩阵

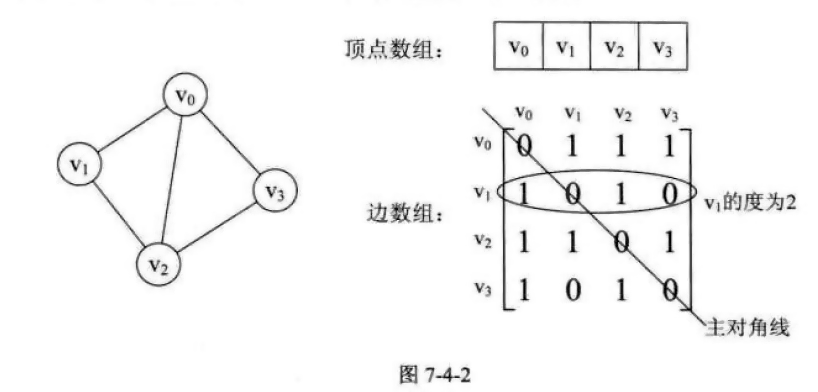
图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

设图G有n个顶点，则邻接矩阵是一个 n * n 的方阵，定义为：

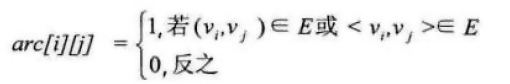
如7-4-2 所示的的无向图及邻接矩阵表示

如7-4-3 所示的的有向图及邻接矩阵表示

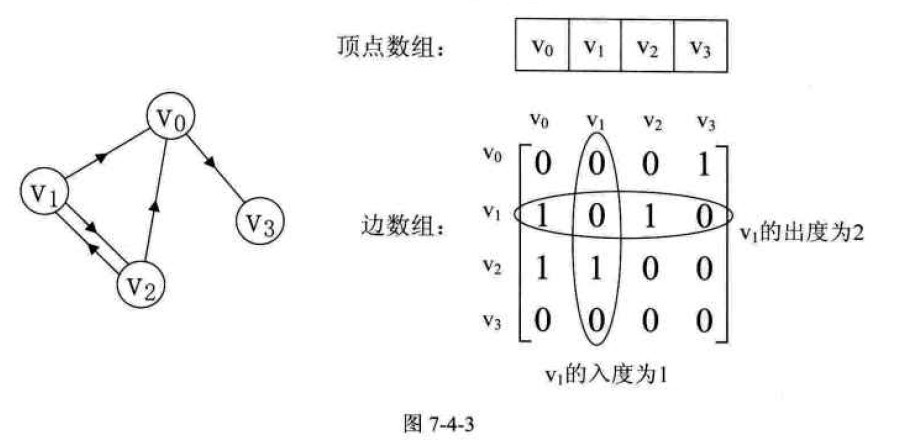
网就是每条边上都带有权的图叫做网。那些这些权值就需要保存下来。设图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

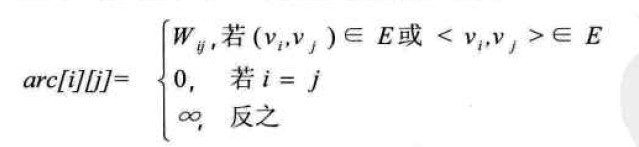
如图7-4-4就是有向网图及其邻接矩阵表示。

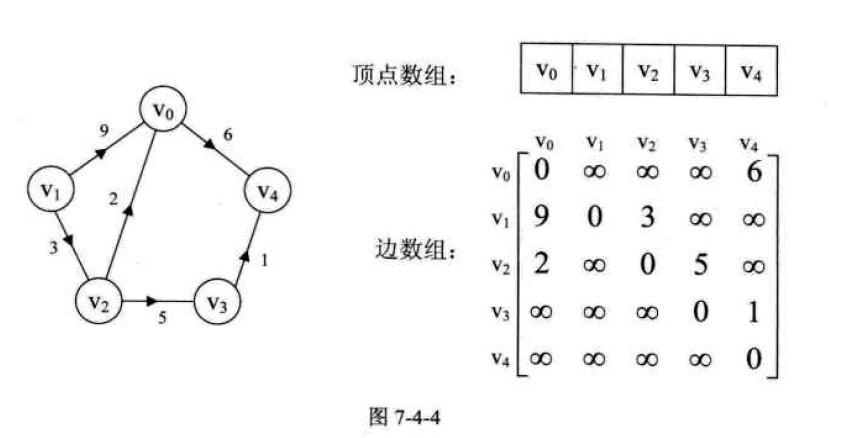
2.2 邻接链表

2.3 十字链表

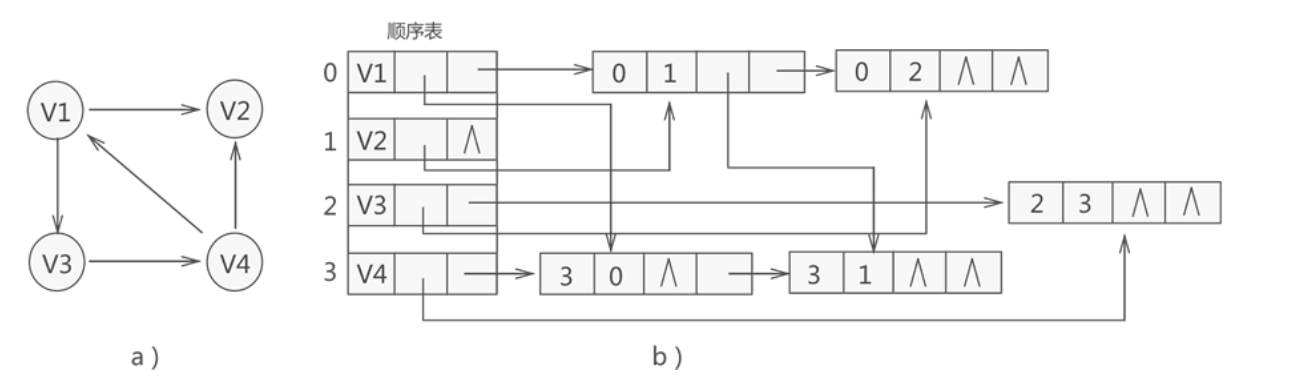
边多的图就是稠密图，例如完全图，一般边多的图用邻接矩阵存储，边少的图用邻接链表存储

3、图的遍历

3.1 深度优先搜索(DFS)

3.2 广度优先搜索(BFS)

最小生成树

最短路径